https://arxiv.org/abs/2006.12770
Pattern Recognitionという雑誌。
Introduction
Domain Adaptationで、2つの分布の距離を近づけようとするだけでは、うまく同じ特徴空間の上に写像するような変換を学ぶのは難しい。これを解決するために、Discriminative Feature Alignment(DFA)という手法を開発した。VAEのように、あるGaussian Priorに揃えるらしい。Source DomainのデータをEncoderで変換したら、ガウス分布になるようにKLダイバージェンスを利用するらしい。
Target DomainのデータをEncoderで変換したものをガウス分布に近づけることには効果はないらしく、代わりにEncoderで変換した表現を再度Decoderで戻したときのL1距離を見るらしい(読むとわかる)
この手法はAdversarialである、ではない両方に応用可能。
この論文の貢献
- Unsupervised Domain Adaptationにおける新たなフレームワークの提案
- Target Domainに対しては、表現をDecoderで復元したあとに、L1距離の最小化をする。
- SOTAの性能を出した。
Related Works
Adversarial Domain Adaptation
敵対的なDomain Adaptationは有効で、識別器がどっちのDomainのデータをEncoderに通して得られた特徴かを知ることができる。Encoderを固定して識別器を訓練→識別器を固定してEncoder、Decoder、本筋のDNNを訓練というループを重ねていく。
Non-adversarial Domain Adaptation
敵対的ではない手法でAlignmentもできる。
- 2つのデータセットの間の平均と共分散の差を、訓練中に埋めるようにする。
- Maximum Mean Discrepancy 2つのドメインの重心を合わせる。
- Source Domainで訓練した識別で、Target Domainのデータに疑似ラベルを用いてTarget Domainでの判別に使う本命の識別器を再学習する。
この論文で提案していたStepwise Adaptive Feature Norm(SAFN)はゆっくり変わっていくので、ドメインシフトがTarget Domain固有の情報のベクトルのノルムは大きいので、ノルムの変化を小さくさせる=共通の知識を学ばせたいらしい。
Auto-encoder
Encoder-Decoderモデルがよくつかわれる。Encoderで抽出したDomainに依存しない特徴を使って、識別器を訓練していく形。Decoderは分布があまり離れないようにするために訓練をする際にだけ使うらしい。
以下のように、Encoderから得た特徴空間の表現と、指定の特徴空間の別の表現をDecoderで復元したときにあまり遠く離れないようにするらしい。
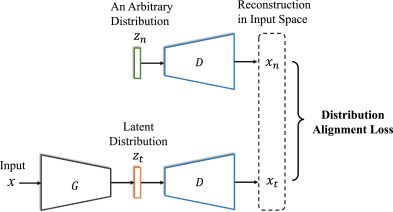
Method
問題設定
- がSource Domainからサンプリングされた個。
- はTarget Domainからサンプリングされた個。
- 目標は、での効率が良い識別器を作ること。
Encoder-Decoderモデルの利用
前述のように、Encoderで抽出した特徴が、Domainに依存しない共通の特徴であるようにしたい。これを用いて、で識別する。
なお、ここではEncoder、Decoderの重みは共有するという正則化をする(簡単なEncoder-Decoderモデルによくある手法)
Encoder-Decoderモデルなので、入れたサンプルとEncoder-Decoderを通し一回特徴にしてから復元したものが同じである方が望ましい。
Target Domainの特徴表現と、Source Domainの特徴表現の(つまりサンプルそのまま)との相互情報量(一方が他方からどれだけ情報をもらっているか)が大きいのが一番うれしい!
これをするためには、Source, Target両方のデータをEncoderで特徴空間にまずマッピングする。このマッピングの際、計算するミニバッチのデータの特徴空間でのマッピングしたときの分布が、ガウス分布と似るようにKLダイバージェンスの制約をかける。
そして、数学的には、ガウス分布にうまく似れば似るほど、相互情報量も大きくなるらしい。
証明
共有情報量はであり、ソースのエントロピーは定数なので、つまりTarget Domainの潜在表現が与えられたときの、Source Domainのデータの条件付エントロピーを最小化することになる。
これは、がうまくの情報をうまく表現している必要がある。この時、ガウス分布に近い形でが整列したら、同じ分散を持つ分布のうち、ガウス分布は最大のエントロピーを持つ分布という性質がある。
つまりもっともランダムな分布で情報を持つものである。これで保持するなら、最も多くの情報を持つことができるようになる。
ガウス分布は一番効率よく情報を貯蔵できる、ということであるが、実際の相互情報量の最大化は以下のようなことを目指す。(条件付エントロピーの定義で展開)
特徴空間でがだいたい同じならば、それはDecoderにかけたときのとなる。
なので、Decoderで変換した際の損失の最小化は以下のようになる。ここで、EncoderとDecoderは同じパラメタを共有していることに注意。
Decoderの構造
基本的に、Pooling以外の層はのように書くことができる。
- 畳み込み これは疎行列の演算として書けるので、を掛けておく転置畳み込みでEncoderとDecoderで同じパラメタを共有して復元、が可能。
- Max Unpooling これは破壊的な情報の抽出なので厳密にはできないが、最大値をとるところ以外は0に設定するというやり方でできる。今回はこのようなやり方でもうまくいく。
- Average Unpooling これは平均値ですべて埋めることにしている。
- 非線形性 非線形性で抽出された特徴のかなりの部分は保持できているらしいので特段気にしなくてよかったらしい。今回の実験ではReLUを使った。
